The model used in the survey
The results presented in this database are obtained as described in reference1.
Structure-based models of proteins are defined through the condition that the lowest energy state of the system coincides with the experimentally determined native structure of a protein and that the solvent is considered only in an implicit way. Such models are usually coarse-grained and the simplest choice is to represent each each amino acid by a bead centered at the Cα atom. There is no unique prescription for a good structure-based model. 62 possible variants have been analysed in ref.3. All of them appear sensible a priori and yet their mechanical and folding properties differ substantially. Several of them match the experimental data on stretching in an optimal way. In this survey, we use the simplest of them. Its description is given below along the lines discussed in references15–17 and, especially, in reference7.
The basic input to modeling involves providing the identity and coordinates of all heavy atoms in each amino acid of the native structure as stored in the PDB2. Each heavy atom is assigned a van der Waals sphere of a radius which is atom-dependent as determined by Tsai et al.8. The radii are enhanced by a factor of 1.24 to account for attractive interactions. In this way, each amino acid is represented by a cluster of spheres. When the cluster corresponding to amino acid i overlaps with that for amino acid j then a native contact is declared to arise. Otherwise, we speak of non-native contacts. Native contacts are attractive and non-native are considered repulsive. Even though the nature of the contact is defined through all heavy atoms, the system is described only by the locations and velocities of the Cα atoms. In the first survey7, all native contacts were included in the energy function. In later works, and, in particular, in reference1 and here we have changed the character of the native i, i + 2 contacts into non-native. The reason is that such contacts usually correspond to the much weaker van der Waals dispersive interactions as can be assessed based on chemical considerations9.
The potential energy, Ep, of the system of residual length N is given by equation:
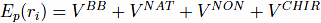
The first term,VBB, is the harmonic potential
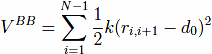
which tethers consecutive beads at the equilibrium bond length. For most pairs, d0 of 3.8 Å. Here, |ri − rj| is the distance between the beads and k = 100ε/Å−2, where ε is defined below.
The native contacts are described by the Lennard-Jones potentials with the uniform energy parameter ε:
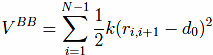
The length parameters, σij in these potentials are selected so that the minima of the po- tentials agree with the experimentally determined distances between the Cα atoms in the contact.
The model also contains a four-body chirality term that favors the native sense of chirality10,
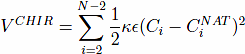
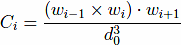
, and CNAT is the chirality of residue i in the native conformation. Here, ωi = ri+1 − ri. A positive Ci corresponds to right-handed chirality. Otherwise the chirality is left-handed. The values of Ci are essentially between -1 and +1. The parameter κ is taken to be equal to 1. The chirality potentials act similar to favoring native values of the dihedral angles3, but we have found it to be computationally more convenient. VCHIR enhances stability of the model and monitoring of chirality is a part of checking of the folding criterion10. The full model considered here is kinetically equivalent11 to the model with the 10-12 contact potentials considered by Clementi et al.12, which was demonstrated to have the two-state kinetics of folding for simple proteins.
The non-native contacts are described by the repulsive part of the Lennard-Jones poten- tials:
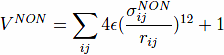
where, σijNON = 4Å corresponds to a repulsive core.
The disulphide bonds are modeled by the harmonic potentials which are similar to the thethering harmonic potentials used to describe the backbone.
The stretching protocol
In our stretching simulations, both termini or selected two amino acids of the protein are attached to harmonic springs of elastic constant k = 0.12ε/Å which is close to the values corresponding to the elasticity of experimental cantilevers (this value corresponds to the "soft" spring case of reference6. The value of k affects the location of the force peaks but it influences their magnitudes only weakly. The free end of one of the springs is anchored while the free end of the second spring is pulled at a constant speed, vp, along the initial end-to-end position vector. We consider vp equal to 0.005 Å/τ , where τ is of order 1 ns since this is a characteristic time to cover a typical distance of 5 Å through diffusion in the implicit solvent. The experimental results are obtained at various speeds that are all at least two orders of magnitude slower. Using one speed for all proteins facilitates making comparisons.
In our simulations, we monitor the force of resistance to pulling, F, as a function of the second spring displacement d. Our main interest is Fmax - the magnitude of the largest force peak as it sets the scale of the force–displacement pattern. Fmax is given in units of ε/Å.
The value of ǫ should be in the range of 800-2300 K since it corresponds to an effective average of all non-covalent interactions in proteins. Our previous simulations of folding16,24 were optimal with the dimensionless temperature T~ = kBT of order 0.3 which corresponds to room temperature if ε is around 900 K (kB is the Boltzmann constant and T is temperature). Our simulations are performed at T~ = 0.3. Our latest estimate of ε is about 110 pNÅ or about 1.5 kcal/mole1. The estimate is based on making comparisons to the experimental values of Fmax and by making logarithmic extrapolations to the experimental pulling speeds, which do not exceed 104 nm/s.
Molecular dynamics
The thermal fluctuations away from the native state are introduced by means of the Langevin noise, i.e. by random Gaussian forces together with a velocity dependent damping. This noise mimics the random effects of the solvent and provides thermostating. Notice though that the ground state of our model corresponds to the native state of the protein that was determined at room temperature.
The equation of motion for each Cα reads
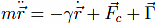
Fc is the net force due to the molecular potentials. The damping constant Γ is taken to
be equal to 2m/τ and the dispersion of the random forces is equal to 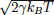 . This choice
of Γ corresponds to a situation in which the inertial effects are negligible5 but the damping
action is not yet as strong as in water. Larger values of γ have only a minor effect on the
F - d curves. The equations of motion are solved by a fifth order Gear predictor-corrector
scheme14 with a time step of 0.005 τ . Due to the overdamping, our results are equivalent to
those obtained by the Brownian dynamics algorithm15.
. This choice
of Γ corresponds to a situation in which the inertial effects are negligible5 but the damping
action is not yet as strong as in water. Larger values of γ have only a minor effect on the
F - d curves. The equations of motion are solved by a fifth order Gear predictor-corrector
scheme14 with a time step of 0.005 τ . Due to the overdamping, our results are equivalent to
those obtained by the Brownian dynamics algorithm15.
In order to account for a finite resolution within which the thermal effects are observed, the F − d curves are averaged over a pulling distance of 0.5 Å.
Dataset preparation
The local PDB mirror was established on December 17, 2008 in order to provide fast and reliable access to all 54 807 entries gathered in PDB at the time. A subset of proteins of sequential length falling between 20 and 250 amino acids was extracted and devoid of non-proteins. It was accomplished by scanning pdb files HEADER sections for words listed in Table I and removing them from the Survey. Subsequent refining steps pruned entries where sequential distance between neighboring amino acids' Cα atoms was outside [3.6 - 3.95] Å range ([2.8, 3.85] Å for cis-proline). This treatment removed both proteins with gaps and proteins with non-native peptide bond length. Presence of artificial amino acids was in principle allowed, special care was taken when dealing with alternative positions of chain fragments and/or side chains. In remaining entries, only first chain/model was taken into account, resulting in total number of 17135 structures.
Table I: Keywords eliminated from the survey
| Keyword | Keyword |
| DNA DUPLEX | DNA/RNAb |
| DNA-BINDING PROTEIN | LYASE/RNA |
| COMPLEX (RIBONUCLEIC ACID/LIGAND) | COMPLEX CDNA |
| COMPLEX (NUCLEOCAPSID) | TRANSCRIPTION DNA |
| NUCLEIC ACID | RIBONUCLEIC ACID |
| DEOXYRIBONUCLEIC ACID | RNA |
| DNA | RIBOSOMAL RNA COMPLEX |
| HYBRID DNA/RNA | OLIGONUCLEOTIDE |
| RIBOSYME | TRNA |
| RIBOSOMES | DEOXYRIBO |
| COMPLEX (NUCLEAR PROTEIN/RNA) |
1 Sikora M, Sulkowska J I, Cieplak M, PLoS Comp Biol 5(10): e1000547 (2009).
2 Berman H M, Westbrook J, Feng Z, Gilliland G, Bhat T N, Weissig H, Shindyalov I N, Bourne P E, Nucl. Acids Res. 28 235-242 (2000).
3 Sulkowska J I, Cieplak M, Biophys. J. 95, 3174-3191 (2008).
4 Hoang T X, Cieplak M, J. Chem. Phys. 112, 6851-6862 (2000).
5 M. Cieplak and T. X. Hoang, Biophys. J. 84 475-488 (2003).
6 M. Cieplak, T. X. Hoang, and M. O. Robbins, Proteins: Struct. Funct. Bio. 56, 285-297 (2004).
7 J. I. Sulkowska and M. Cieplak, J. Phys.: Cond. Mat. 19, 283201 (2007).
8 J. Tsai, R. Taylor, C. Chothia, and M. Gerstein, J. Mol. Biol. 290 253-266 (1999).
9 Sobolev V, Sorokine A, Prilusky J, Abola E E, Edelman M, Bioinf. 15, 327-32 (1999).
10 J. I. Kwiecinska and M. Cieplak. J. Phys.: Cond. Mat. 17 S1565-S1580 (2005).
11 M. Cieplak and T. X. Hoang, Physica A 330, 195-205 (2003).
12 C. Clementi, H. Nymeyer, and J. N. Onuchic, J. Mol. Biol. 298, 937 (2000).
13 M. Cieplak and T. X. Hoang, Proteins: Structure, Function and Genetics 44 20-25 (2001).
14 W. C. Gear, Prentice-Hall, Inc. (1971).
15 D. L. Ermak and J. A. McCammon, J. Chem. Phys., 69, 1352 (1978).

